I am an applied mathematician studying machine learning, data science and multi-linear algebra. My research centers on scalable methods and statistical properties of high-dimensional inverse problems, that include tensor decomposition, scientific machine learning and cryo-electron microscopy. In addition, I have interests in machine learning, deep learning, statistics, information theory and optimization.

​ I am an Assistant Professor in the Department of Mathematics at the University of Georgia. I was a Ph.D. student of Emmanuel Abbe and Amit Singer at Princeton University and worked as a postdoc with Vahid Tarokh at Duke University, and with Joe Kileel and Rachel Ward at University of Texas at Austin. Before joining UGA, I was an Assistant Professor at Instituto de Matemática Pura e Aplicada (IMPA), in Rio de Janeiro, Brazil.

Research ProjectsProjetos de Investigação

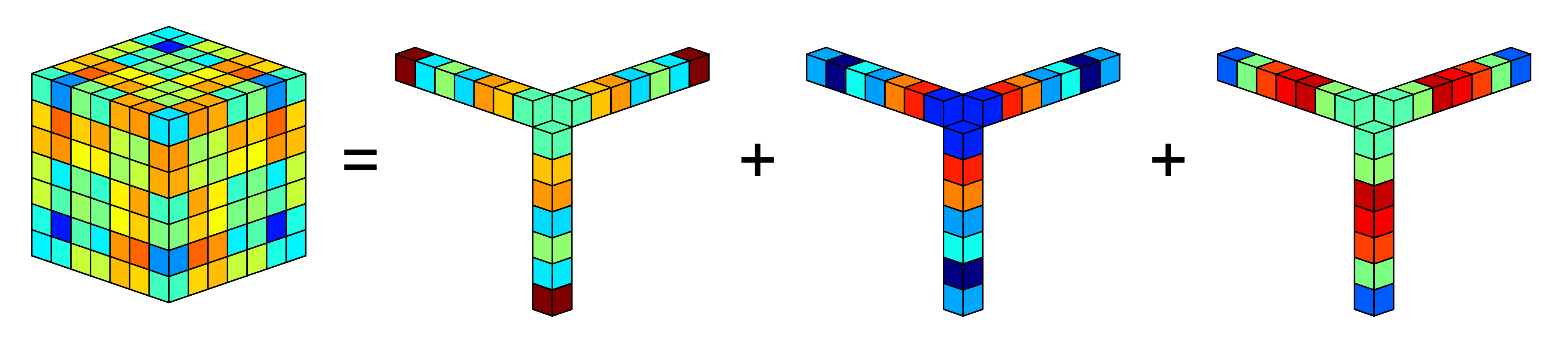
Tensor Decompositions
I develop and analyze algorithms for decomposing tensors, with special focus on symmetric and partially symmetric tensors. These tensors often arise in applications as
  • Statistical moments (higher-order covariances)
  • Derivatives (higher-order Hessians)
  • Hypergraphs (higher-order adjacency tensors)
I am particularly interested in developing implicit tensor decomposition algorithms, that decompose tensors without explicitly forming them.

Relevant papers: [14] [13] [10]

Recorded Talk: Method of Moments: From Sample Complexity to Efficient Implicit Computations

Illustration of symmetric tensor decomposition.
Credit: João M. Pereira
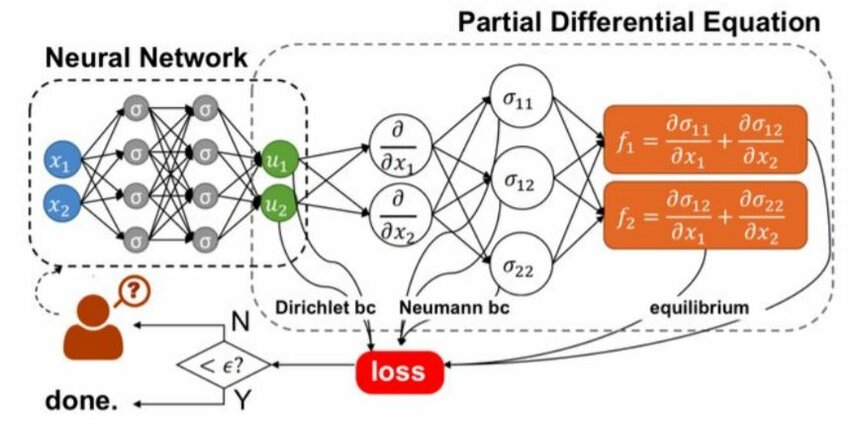
Scientific Machine Learning
I develop and analyze machine learning methods for learning and solving ordinary, partial and stochastic differential equations. My research includes developing new physics-informed architectures that encode key properties of differential equation solutions, as opposed to enforcing these properties through added losses, as in traditional physics-informed architectures.

Relevant papers: [18] [15] [11] [9]

Recorded Talk: Learning Laws of datasets

Schematic of PINNs. The loss includes terms that enforce the PDE in sample points. The derivatives are evaluated exactly and efficiently using autograd.
Credit: Aviral Chharia et al.
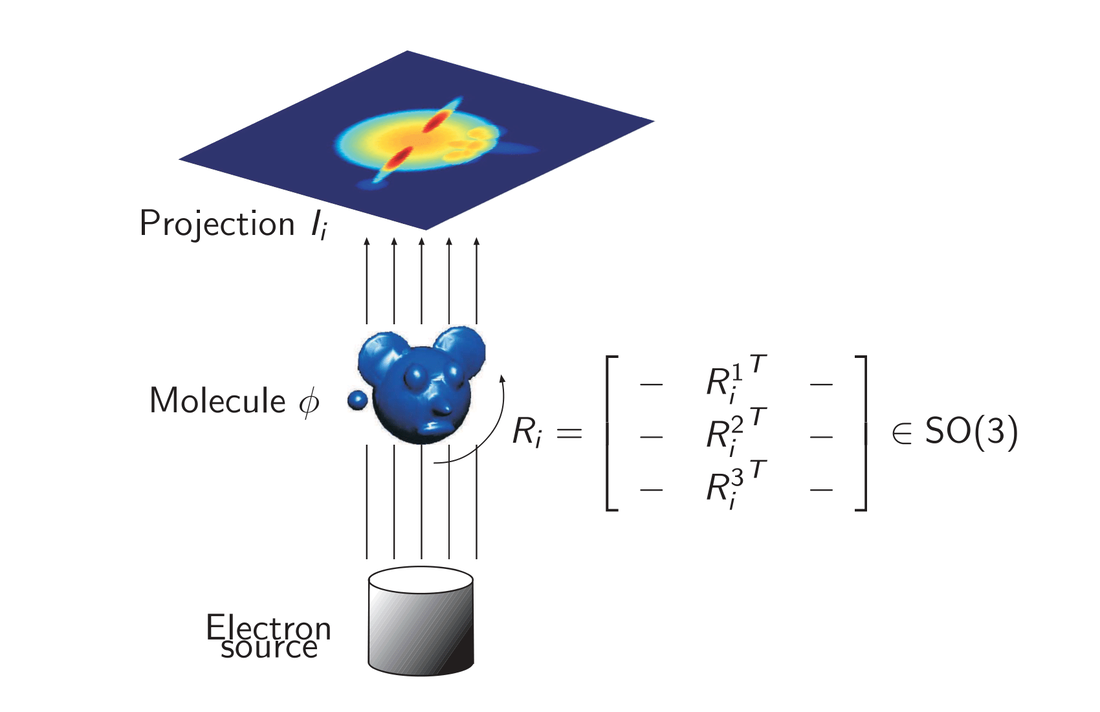
Fundamental Limits of multireference alignment and Cryo-EM
Cryo-electron microscopy (cryo-EM) is a technique to determine the 3D structure of molecules. A crucial challenge in cryo-EM consists of estimating the 3D electrostatic potential of the molecule from (very noisy) 2D projections of the molecule potential, over unknown viewing directions. This problem can be seen as an instance of MRA, where the observations result from a group action on the signal, which is then corrupted with noise. I study the fundamental limits of multireference alignment (MRA) in the low signal-to-noise ratio (SNR) regime, which is the prevalent regime in cryo--EM this context. We have showed previously that the sample complexity, that is, the number of samples needed to achieve a certain level of accuracy, is determined by the lower order moments of the data.

Relevant papers: [7] [6] [5]

Single-particle reconstruction problem in Cryo-EM
Credit: Amit Singer
Pseudo-spectra of Time-Frequency localization operators
I have a long-standing ongoing project studying time-frequency localization operators. Previously, we have used inequalities arising from the trace and norm of time-frequency localization operators to study their pseudo-spectra and obtain other important results. Moreover, we used similar ideas to show that a class of determinantal point processes, associated with the Schrödinger representation of the Heinsenberg group, belong to a state of matter called hyperuniform.

Relevant papers: [16] [4] [3] [2] [1]

Left: Poisson process, not uniform;
Middle: hyperuniform;
Right: Lattice/Crystal, also hyperuniform.
Credit: Wikipedia

PublicationsPublicações

[18]      A. Bizzi, L. Nissenbaum, and J. M. Pereira,
Neural conjugate flows: A physics-informed architecture with flow structure,
Proceedings of the AAAI Conference on Artificial Intelligence, vol. 39, no. 15, pp. 15 576–15 586, Apr. 2025.

[17]      M. M. Alves, J. M. Pereira, and B. F. Svaiter,
A search-free \(O(1/{k}^{3/2})\) homotopy inexact proximal-Newton extragradient algorithm for monotone variational inequalities,
SIAM Journal on Optimization, vol. 34, no. 4, pp. 3235–3258, 2024.
[preprint] [code]

[16]      L. D. Abreu and J. M. Pereira,
Orthonormal functions with prescribed time-frequency localization,
ResearchGate pre-print, 2023.

[15]      A. Hasan, K. Elkhalil, Y. Ng, J. M. Pereira, S. Farsiu, J. Blanchet, and V. Tarokh,
Modeling extremes with \(d\)-max-decreasing neural networks,
in Proceedings of the Thirty-Eighth Conference on Uncertainty in Artificial Intelligence, vol. 180. PMLR, 01–05 Aug 2022, pp. 759–768.
[preprint] [code]

[14]      J. M. Pereira, J. Kileel, and T. G. Kolda,
Tensor moments of Gaussian mixture models: theory and applications,
ArXiv preprint, arXiv:2202.06930, 2022.
[code]

[13]      J. Kileel, T. Klock, and J. a. M Pereira,
Landscape analysis of an improved power method for tensor decomposition,
in Advances in Neural Information Processing Systems, vol. 34, 2021, pp. 6253–6265.

[12]      A. Hasan, K. Elkhalil, J. M. Pereira, S. Farsiu, J. H. Blanchet, and V. Tarokh,
Deep extreme value copulas for estimation and sampling,
ResearchGate pre-print, 2021.

[11]      A. Hasan, J. M. Pereira, S. Farsiu, and V. Tarokh,
Identifying latent stochastic differential equations,
IEEE Transactions on Signal Processing, vol. 70, pp. 89–104, 2022.
[preprint] [code]

[10]      J. Kileel and J. M. Pereira,
Subspace power method for symmetric tensor decomposition,
ArXiv preprint, arXiv:1912.04007, 2019.
[code]

[9]      A. Hasan, J. M. Pereira, R. Ravier, S. Farsiu, and V. Tarokh,
Learning partial differential equations from data using neural networks,
in ICASSP 2020 - 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2020, pp. 3962–3966.
[preprint] [code]

[8]      Y. Ng, J. M. Pereira, D. Garagic, and V. Tarokh,
Robust marine buoy placement for ship detection using dropout k-means,
in ICASSP 2020 - 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2020, pp. 3757–3761.
[preprint]

[7]      E. Abbe, T. Bendory, W. Leeb, J. M. Pereira, N. Sharon, and A. Singer,
Multireference alignment is easier with an aperiodic translation distribution,
IEEE Transactions on Information Theory, vol. 65, no. 6, pp. 3565–3584, 2019.
[preprint] [code]

[6]      E. Abbe, J. M. Pereira, and A. Singer,
Estimation in the group action channel,
in 2018 IEEE International Symposium on Information Theory (ISIT), June 2018, pp. 561–565.
[preprint]

[5]      E. Abbe, J. M. Pereira, and A. Singer,
Sample complexity of the Boolean multireference alignment problem,
in 2017 IEEE International Symposium on Information Theory (ISIT), 2017, pp. 1316–1320.
[preprint]

[4]      L. D. Abreu, J. M. Pereira, and J. L. Romero,
Sharp rates of convergence for accumulated spectrograms,
Inverse Problems, vol. 33, no. 11, p. 115008, 2017.
[preprint]

[3]      L. D. Abreu, J. M. Pereira, J. L. Romero, and S. Torquato,
The Weyl–Heisenberg ensemble: hyperuniformity and higher Landau levels,
Journal of Statistical Mechanics: Theory and Experiment, no. 4, p. 043103, 2017.
[preprint]

[2]      L. D. Abreu and J. M. Pereira,
Pseudo prolate spheroidal functions,
in 2015 International Conference on Sampling Theory and Applications (SampTA), 2015, pp. 603–607.
[preprint]

[1]      L. D. Abreu and J. M. Pereira,
Measures of localization and quantitative Nyquist densities,
Applied and Computational Harmonic Analysis, vol. 38, no. 3, pp. 524–534, 2015.
[preprint]

João M. Pereira